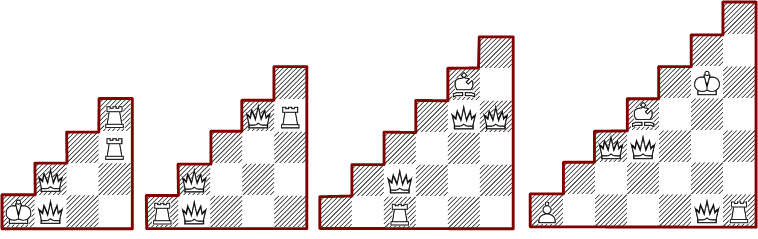
Auf verschieden großen Schachbrettern werden Figuren einer Farbe so gesetzt, daß alle Felder genau zweimal gedeckt sind. Im Gegensatz zu den sehr übersichtlichen einfachen Deckungen entfaltet sich ein großer Reichtum an Formen, was man schon an der deutlich größen Anzahl von Anordnungen erkennt.
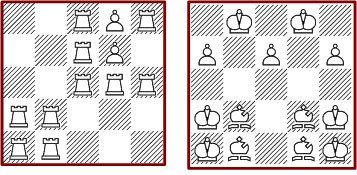
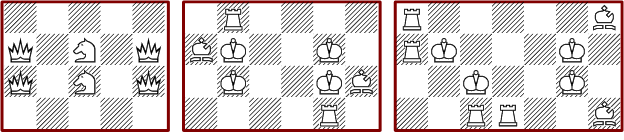
Von den insgesamt 1242 verschiedenen Lösungen bestehen 34 ausschließlich aus den Hauptfiguren. Unten sind die vier minimalen mit 6 und eine maximale mit 14 Figuren zu sehen.

Es gibt eine einzige vollständig symmetrische Form und zwei doppelt spiegelbare Anordnungen.

Interessant sind auch noch die beiden Anordnungen, die nur aus Springern bestehen und die einzige Lösung mit Bauern und Damen.
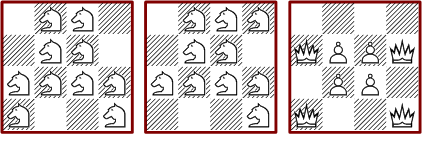
Die Verteilung der Figuren ist folgendermaßen:
| Figuren | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Lösungen | 4 | 9 | 59 | 147 | 324 | 336 | 264 | 85 | 14 |
Gesamtzahl: 1242, davon 49 symmetrisch
Liste aller Lösungen
Es gibt vier minimale Anordnungen mit acht Figuren. Die markierten Türme im zweiten Bild können zwei alternative Positionen einnehmen. Die maximale Anordnung ist eine von vielen.
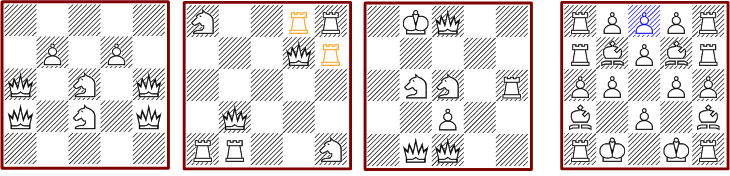
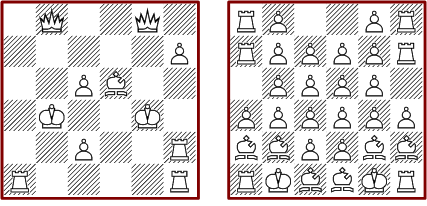
Von den doch recht vielen Lösungen sind nur zehn ohne Bauern möglich. Nur eine davon hat keinerlei Symmetrie.
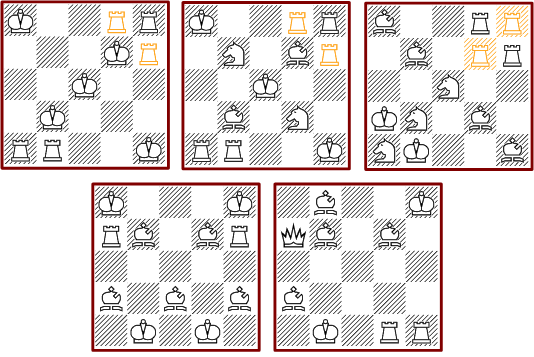
Die nächste beiden Diagramme zeigen Anordnung, welche mit weniger Figuren nur eine einzige Lösung haben. Die Anordnung mit Türmen und Bauern erfährt im Abschnitt »Erweiterbare Lösungen« eine besondere Bedeutung.
Die Verteilung der Lösungen nach Figurenzahl zeigt immer deutlicher, daß Lösungen mit vielen Figuren ähnlich schwierig zu finden sind, wie die mit wenigen.
| Figuren | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Lösungen | 4 | 13 | 20 | 115 | 287 | 581 | 830 | 929 | 691 | 371 | 172 | 66 | 9 |
Die Gesamtzahl ist 4088, davon sind 263 symmetrisch.
Liste aller Lösungen (0,25MB)
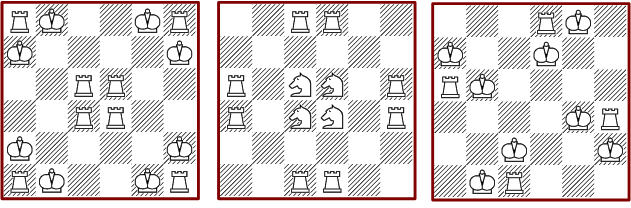
Bei der doppelten Deckung wächst die Anzahl der Lösungen rasant mit der Größe der Bretter. Die gesamte Lösungsmenge ist bei 6*6 aber noch vollständig berechenbar. Die minimale Anordnung besteht aus elf Figuren und ist erstanlicherweise auch die einzig mögliche. Von maximalen Anordnungen mit 32 Figuren gibt es mehrere.
Die Anzahl der Lösungen ohne Bauern bleibt mit 12 dennoch
übersichtlich.
Es gibt zwei voll symmetrische Formen und eine drehsymmetrische.
Von den doppelt spiegelbaren Lösungen gibt es acht.
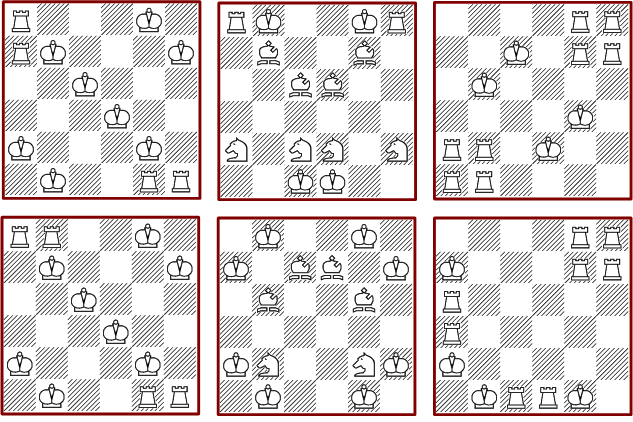
Zwei weitere Anordnungen bestehen nur aus Türmen, die den Grundstein zu erweiterbaren Lösungen bilden (siehe weiter unten).
Im nächsten Bild sind die Lösungen jeweils mit den verwendeten Figuren die einzig möglichen.
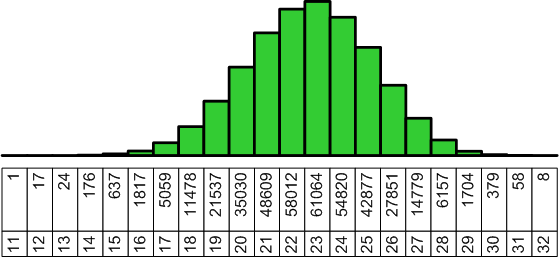
Hier die obligatorische Verteilung der Lösungen nach Anzahl der Figuren, diesmal in grafischer Form. Man erkennt deutlich, daß die Lösungen sehr regulär verteilt sind. Ich verstehe dies als Hinweis auf eine generelle Eigenschaft dieser Problemklasse.

Insgesamt gibt es 392.091 Lösungen, davon sind 658 symmetrisch.
Die Tiefe des Suchbaum ist bereits so groß, daß es nur Teilergebnisse
gibt. Für die Anfangssituation ![]() B3
und
B3
und ![]() C2
gibt es bereits +25.000 Lösungen, die alle mehr als 21 Figuren
benötigen und damit mehr als die weiter unten beschriebene erweiterbare
Lösung.
C2
gibt es bereits +25.000 Lösungen, die alle mehr als 21 Figuren
benötigen und damit mehr als die weiter unten beschriebene erweiterbare
Lösung.
Da gibt es noch viel zu tun.
Noch nicht erforscht.
Die folgenden erweiterbaren Lösungen für doppelte Deckung leiten sich alle aus Viererblöcken von Türmen ab.
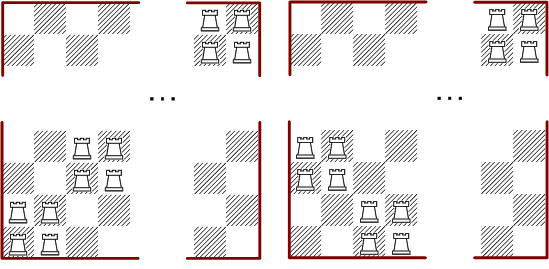
Mit dieser Methode lassen sich doppelte Deckungen für alle quadratischen Bretter mit gerader Feldzahl konstuieren. Da sich die Richtung der Diagonalen vielfach mischen läßt, entsteht eine ganze Familie von erweiterbaren Lösungen, die jedoch alle auf dem gleichen Prinzip beruhen.
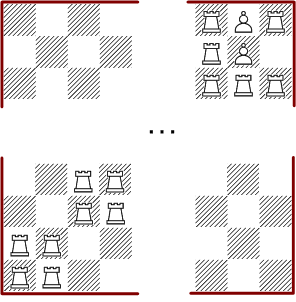
Jede der durch das obige Verfahren hergestellten Lösung kann man zusätzlich um drei Spalten und Reihen erweitern, wie dieses Diagramm zeigt. Damit hat man auch für alle ungeraden quadratischen Bretter eine Lösung.
Gibt es noch mehr erweiterbare Lösungen ?
Die minimalen rechteckigen 3*n-Bretter sind meist auch minimale Lösungen der n*3-Bretter. Ausnahmen sind wegen der verwendeten Bauern 8*3, wobei sogar noch eine Figur mehr benötigt wird, und das 9*3 und 11*3 Brett.
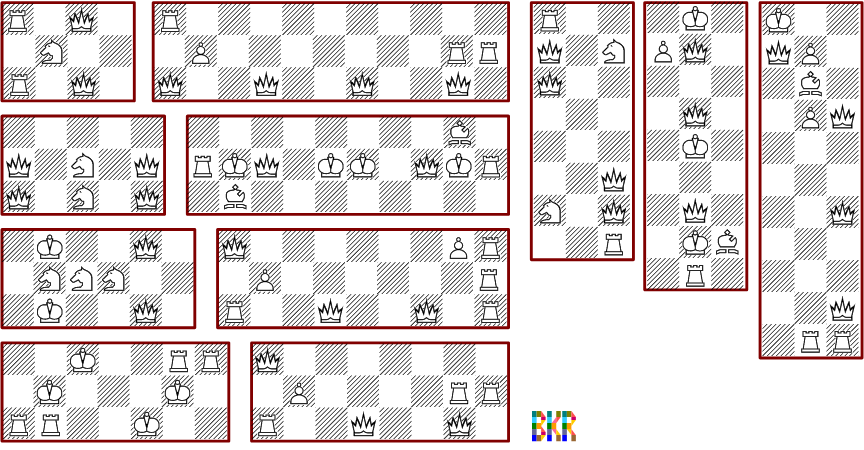
Das folgende Bild zeigt einige minimale Lösungen für rechteckige 4*n-Bretter:
Minimale Lösungen für Diamantformen:
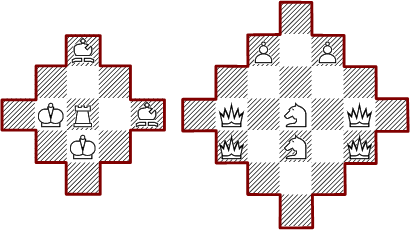
Minimale Lösungen für Dreiecksformen: