Hier werden Schachfiguren einer Farbe so gesetzt, daß alle Felder genau dreimal gedeckt sind. Dieses Problem ist im Vergleich zu den ein- und zweifachen Deckungen sehr komplex und führt schon beim 6x6 Brett an den Rand der praktischen Berechenbarkeit, zumindest für mich.
Die 744 verschiedenen Lösungen des 4*4 Bretts, teilen sich in 121 nur mit den Hauptfiguren und 623 Lösungen mit Bauern auf. Es gibt eine einzige minimale Anordnung mit acht Figuren.

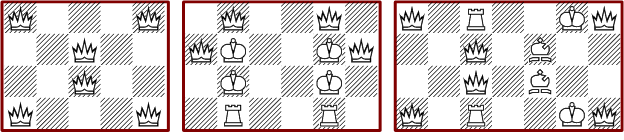
Nur beim 4*4 Brett ist es möglich, daß die maximalen Anordnungen das Brett vollständig auszufüllen. Das folgende Bild zeigt sämtliche möglichen Lösungen dieser Art.

Die Verteilung der Figuren ist folgendermaßen:
| Figuren | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Lösungen | 1 | 6 | 25 | 84 | 177 | 204 | 164 | 65 | 18 |
Gesamtzahl: 744, davon 57 symmetrisch
164 Lösungen verwenden alle Figurenarten.
Liste aller Lösungen
Das nächste Diagramm zeigt alle zehn minimale Anordnungen mit elf Figuren. Die farbig markierten Figuren sind gegeneinander austauschbar.
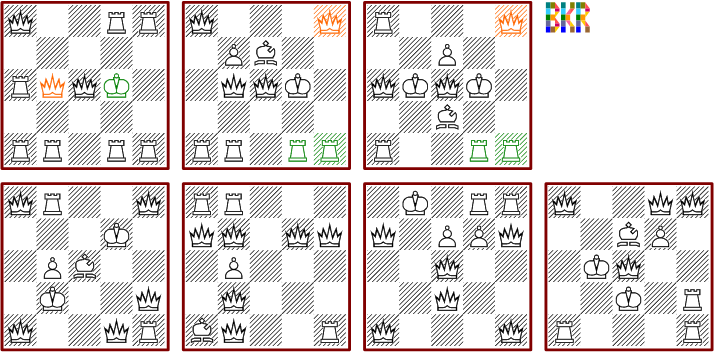
Die Anzahl der Lösungen ohne Bauern beträgt 425, das macht 1,5% aus. Die nächste beiden Diagramme zeigen Anordnungen, welche mit den verwendeten Figurenarten nur eine einzige Lösung haben.

Verteilung nach Figurenzahl:
| Figuren | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| Lösungen | 10 | 24 | 128 | 553 | 1667 | 3282 | 5423 | 6365 | 5846 | 3823 | 1779 | 328 |
Die Gesamtzahl ist 29.228, davon sind 30 symmetrisch.
10.269 Lösungen verwenden alle Figurenarten.
Liste aller Lösungen (ZIP 0,3MB)
Die Anzahl der Lösungen wächst für die dreifache Deckung explosionsartig an, sodaß es derzeit nur Zwischenergebnisse gibt. Diese Anordnung mit 16 Figuren ist das zur Zeit bekannte Minimum.

Noch nicht erforscht.
Es sind bisher keine erweiterbaren Lösungen für Dreifachdeckung bekannt.
Die minimalen rechteckigen 3*n-Bretter, welche auch für n*3 minimal sind ...
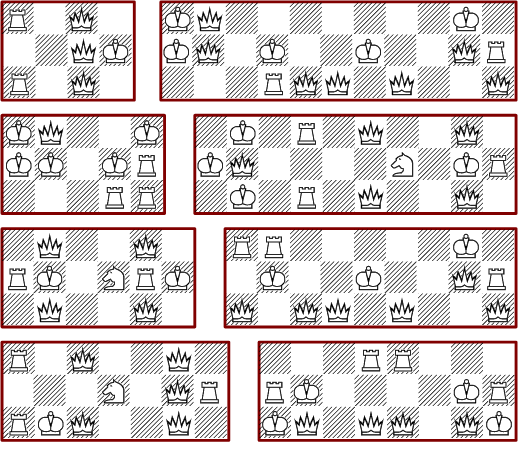
Das folgende Bild zeigt einige minimale Lösungen für rechteckige 4*n-Bretter:
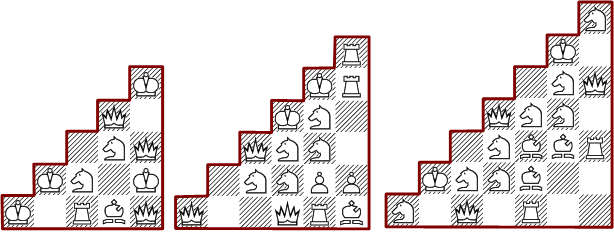
Diese Diamantformen haben 97 und 134.717 verschiedene Lösungen, wobei die minimale Anordnung mit den vier Stufen die einzige ist.
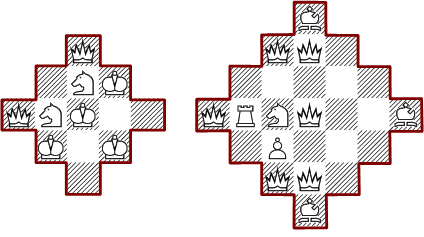
Die Suche nach den Lösungen mit Dreiecksformen ergab, daß für die Vierertreppe gar keine Lösungen existieren. Die unten gezeigten Anordnungen für die größeren Treppen sind jeweils mit den wenigsten möglichen Figuren hergestellt.