In diesem nächsten Schritt werden Schachfiguren einer Farbe so gesetzt, daß alle Felder genau viermal gedeckt sind. Die Berechenbarkeit wird nun wieder einfacher, da sich die Deckungsmuster schnell überschneiden. Die Anzahl der Lösungen ist dann auch recht klein.
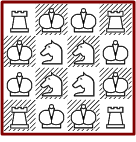
Die einzig mögliche Anordnung mit vierfacher Deckung auf dem 4*4 Brett ist zudem noch vollständig symmetrisch.

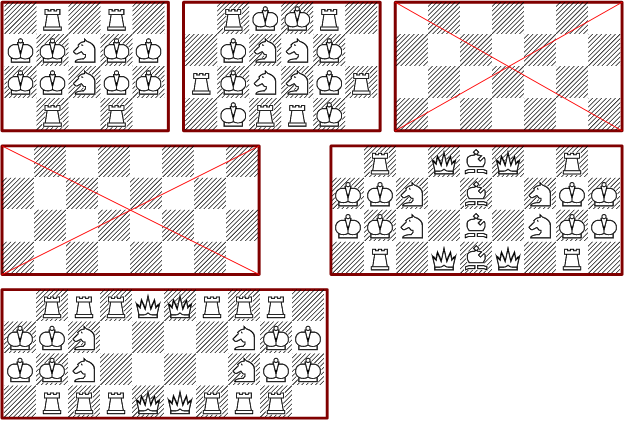
Alle elf möglichen Anordnungen von Schachfiguren, die das 5*5 Brett vollständig vierfach decken, sind im nächsten Bild zu sehen. Es sind mindestens 19 Figuren notwendig. Keine der Lösungen enthält Bauern. Interessant ist, daß sich eine Gruppe von fünf Springern immer an der gleichen Position befindet.
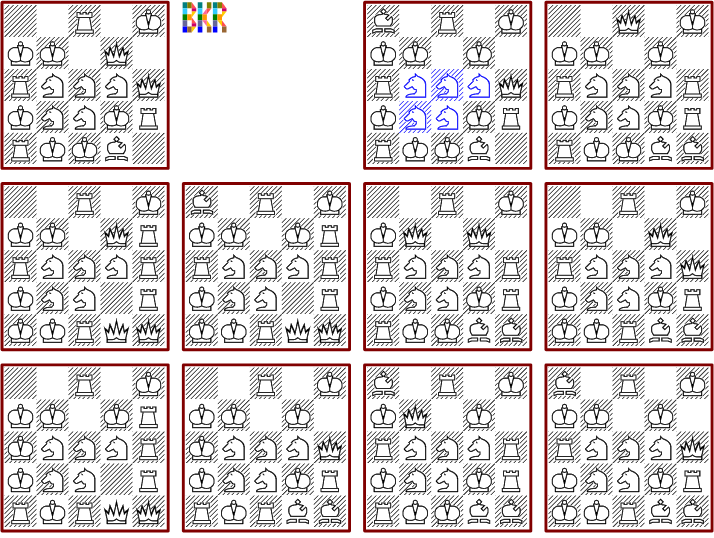
Auf dem 6*6 Brett gibt es lediglich acht verschiedene Stellungen, die alle Felder vierfach decken. Diese geringe Anzahl ist schon erstaunlich, sie ist sogar kleiner als die Zahl des 5*5 Brettes. Eine der Lösungen besteht aus 26 Figuren, alle anderen benötigen 28 bis 30 Figuren. Neben der minimalen Anordnung sind drei weitere Lösungen symmetrisch. Die unteren sechs Stellungen zeichnen sich durch eine markante ringförmige Springerstruktur im Zentrum aus.
Noch nicht erforscht.
Es sind bisher keine erweiterbaren Lösungen für Dreifachdeckung bekannt.
Die minimalen rechteckigen 3*n-Bretter sind soweit berechnet auch minimale Lösungen der n*3-Bretter. Einige dieser Formate haben nachgewiesenermaßen gar keine Lösungen mit vierfacher Deckung.
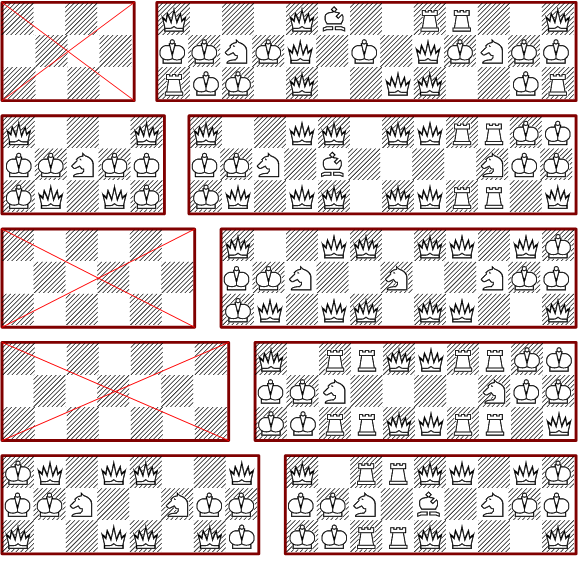
Das folgende Bild zeigt einige minimale Lösungen für rechteckige 4*n-Bretter:
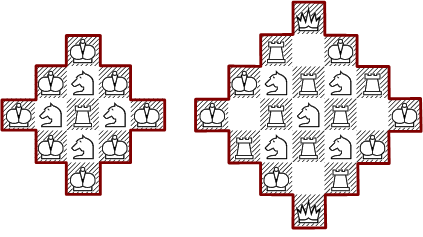
Minimale Anordungen für Diamantformen:
Eine vierfache Deckung von Dreiecksformen ist nicht möglich. Man sieht das sofort, wenn man versucht, die Eckfelder zu decken.