Da das Schachspiel schon sehr alt ist, wurden im Laufe der Zeit auch viele Schachrätsel erfunden, die mit dem eigentlichen Spiel nur entfernt zusammenhängen. Dieses Kapitel befaßt sich mit einem solcher Rätsel.

Der Anstoß zu den folgenden Seiten entstand aus den Versuchen, das »Problem of the Month July 2006« von Erich Friedman zu lösen. Dort wird die Frage gestellt, wie man ein n*m Felder großes rechteckiges Schachbrett derart mit weißen Schachfiguren besetzen kann, daß jedes Feld genau k-mal von den Figuren gedeckt wird. Diese Bedingung gilt für besetzte und unbesetzte Felder in gleicher Weise. Die Kenntnis der Regeln, wie Schachfiguren schlagen, sind zum weiteren Verständnis notwendig und werden als bekannt angenommen.

Jede Schachfigur kann beliebig oft und an jeder Stelle gesetzt werden, natürlich nur jeweils eine Figur auf einem Feld. Die Besonderheiten der Bauern wie Umwandlung auf der letzten Reihe und das Schlagen en-passant werden außer Betracht gelassen. Diese dürfen auf jedem Feld, also auch auf der ersten und letzten Reihe gesetzt werden. Mit »k-mal gedeckt« sind, um es genau zu definieren, nur die k direkten Angriffe auf ein Feld zu zählen. Dies ist ein etwas anderes Verständnis, als es ein Schachspieler hat, der die Felder vor einem Doppelturm als zweifach gedeckt zählt.

Mit diesen Regeln ist ein interessantes und recht schwieriges Puzzel beschrieben, welches nun genauer untersucht wird. Das Puzzel ist vom Problemtyp der vollständigen Überdeckung wie es auch Polyform Puzzel sind. Jedoch ist das Verhalten der Figuren dynamisch und hängt von deren Kontext ab. Bei der ursprünglichen Frage von Erich Friedman ging es vorrangig um die minimalen Lösungen, d.h. diejenigen mit den wenigsten Figuren. Hier wird die Materie vertieft analysiert, wobei einiges Interessante zutage kommt.

Etliche der Lösungen für 2*2 und 3*3 Felder kann man noch finden, indem man das hölzerne Schachbrett aus dem Regal nimmt und probiert.

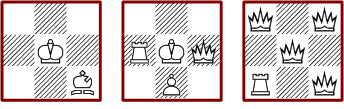
Ein- zwei- und dreifache Deckung

Die Grafiken entstanden im übrigen mit einem Schach-Font von Eric Bentzen, welcher den Figuren der Bücher des Sportverlag Berlin nachempfunden ist. Dieser Verlag hat zu Zeiten der DDR Übersetzungen von erstklassigen russischen Schachbüchern herausgebracht, mit denen ich in meiner Jugendzeit mit großem Erfolg Schachtaktik geübt habe.

Doch selbst bei diesen Miniaturschachbrettern ist es sehr mühsam, alle Lösungen händisch zu finden. Dazu bedarf es einiger Überlegungen zu einem Verfahren, welches dann zu der vollständigen Aufzählung aller vorkommenden Lösungen führt. Die Obergrenze der Anzahl der Figurenanordnungen liegt bei 7^n*m, nämlich jeweils sechs verschiedene Figuren oder ein freier Platz auf jedem Feld. Das ist schon bei einem 5*5 Brett eine viel zu große Zahl, um alle Möglichkeiten plump mit einem Rechner durchprobieren zu lassen.

Man braucht also ein Verfahren, welches das Brett Feld für Feld füllt. Der erste Ansatz, die Felder der Reihe nach mit Figuren zu besetzen, bis ein Feld mehr als k-mal gedeckt ist, taugt leider nicht. Denn die Abbruchbedingung ist nicht gültig, da bei den fernwirkenden Figuren die Angriffslinien durch weitere Figuren wieder unterbrochen werden könnten.

Dazu diese Illustration:
Auf dem 5*5 Brett sollen alle Felder zweifach gedeckt werden. Die Figuren werden in der Reihenfolge von unten nach oben und von links nach rechts gesetzt. Beim Setzen des Läufers auf c1 wird das Feld a3 bereits dreifach gedeckt. Nun darf man daraus nicht schließen, daß die Position des Läufers nicht gültig ist, denn eine Figur auf dem blau markierten Feld b2 heilt die Situation wieder. Damit ist man in Verlegenheit, eine Bedingung für das reihenfolgeweise Setzen von Figuren zu finden. Ich weiß jedenfalls keine.

Aus diesen Vorüberlegungen entstand die Idee, die Sache von der fertigen Lösung her zu betrachten. Denn jede Lösung läßt sich in eine Anzahl von Figuren mit ihren gedeckten Feldern zerlegen. Das heißt man betrachtet statt der Figuren ihre Deckungsmuster. Darunter versteht man eine Anordnung von angegriffenen Feldern zusammen mit dem begrenzenden Kontext. Die Deckungsmuster sind also Lösungsfragmente, die in ihrer Summe die Lösung bilden. Gerade die fernwirkenden Figuren erzeugen eine Vielzahl von solchen Mustern, je nach freiem Platz in ihrer Nähe. Die Deckungsmuster einer Figur hängen von der Form und Größe des Bretts, der Lage und Umgebung der Figur ab. Sie müssen also für jede Konfiguration neu berechnet werden. Jedes der folgenden Diagramme zeigt genau ein Deckungsmuster.

Auch dazu einige Illustrationen:
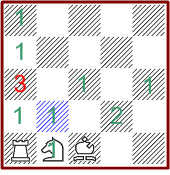
Die Muster von Springern, Königen und Bauern sind einfach zu verstehen, da diese Figuren keine Fernwirkung haben und somit die Muster nicht von benachbarten Figuren abhängen. Für jede Brettposition entsteht deshalb genau ein Muster.

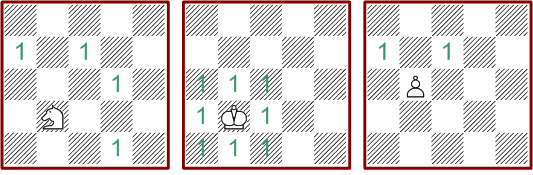
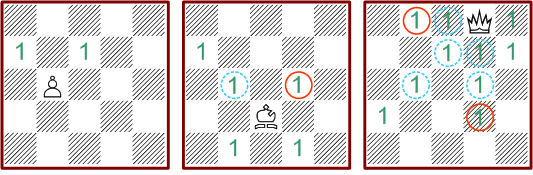
Der Läufer als fernwirkende Figur hat nun an jeder Brettposition mehrere mögliche Muster. Das Diagramm links zeigt verschiedene Muster die vorkommen, wenn auf den Feldern mit den roten Ringen irgendeine andere Figur steht und die Felder mit den blauen Ringen frei sind. Der Läufer hat also in der gezeigten Position vier mögliche Deckungsmuster. Figuren auf den Randfeldern haben hier keinen Einfluß.

Auf dem 5*5 Brett haben die Könige, Springer und Bauern haben jeweils 25 Muster, die Läufer 95, die Türme 324 und die Dame als flexibelste Figur hat 1331 Deckungsmuster.

Jedes Deckungsmuster läßt sich durch vier Typen von Statusinformation beschreiben, wobei die Typen 3 und 4 nur als Zusatzinformation des Typs 2 vorkommen können.

1. die Position der Figur (Symbol)
2. die abgedeckten Felder (grüne Anzahl)
3. von Figuren freizuhaltende Felder (blauer Kreis)
4. mit Figuren zu besetzende Felder (roter Kreis)

Die Deckungsmuster lassen sich unter bestimmten Bedingungen durch Addition kombinieren. Natürlich darf man wie beim klassischen Schachspiel auf jedes Feld nur eine einzige Figur setzen. Es dürfen Felder vom Typ 1 nicht mit Typ 3 kombiniert werden, also keine Figuren auf freizuhaltende Felder plaziert werden. Weiterhin schließen sich Typ 3 und 4 wechselseitig aus.

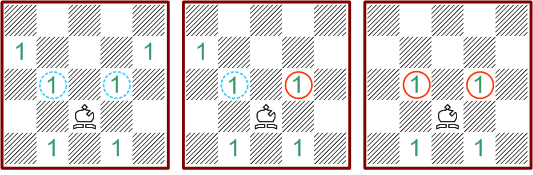
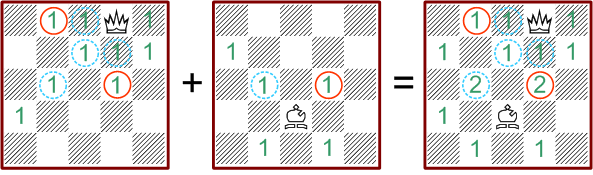
Beispiele:

Diese drei Muster sind alle untereinander inkompatibel. Der Bauer würde freizuhaltende Felder besetzen. Das Deckungsmuster des Läufers fordert eine Figur auf dem Feld d3, welches durch die Dame blockiert ist.

Dafür nun eine Folge von erlaubten Additionen, deren Ergebnis auch immer reihenfolgeunabhängig ist.

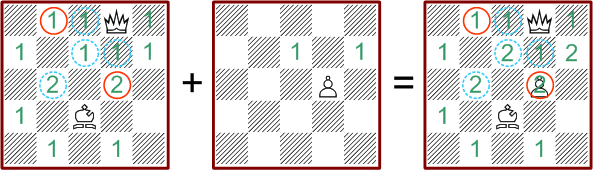
Jede Lösung eines Schachpuzzels läßt sich eindeutig als Summe von aufaddierten Deckungsmustern beschreiben.

Mit diesen Vorüberlegungen ist das Verfahren zur Lösung nun ganz einfach, dabei beschränken wir uns erstmal auf Deckungsprobleme mit einfacher Deckung.

Zuerst erzeugt man wie oben beschrieben sämtliche Deckungsmuster aller Figuren. Dann legt man eine Reihenfolge der Felder fest, in welchen man vorgehen will. Die Art der Reihenfolge ist egal, sie darf nur unterwegs nicht verändert werden. Damit bekommt jedes Feld eine Nummer von 1 bis n*m. Nun wird für alle Muster die kleinste Feldnummer ermittelt, welche durch das Muster gedeckt wird (Typ 1). Umgekehrt ist damit jedem Feld eine Liste von Deckungsmustern zugeordnet.

Man beginnt nun mit dem ersten Feld und dem ersten Muster in der Liste, welches ja mindestens dieses Feld deckt. Dann geht man jeweils zum nächsten Feld, verfährt ebenso und addiert das Muster auf das vorhandene. Wenn die Muster kompatibel sind und kein Feld mit mehr als einer Deckung entsteht, geht man zum nächsten Feld und andernfalls versucht man das nächste Muster in der Liste zu setzen. Wenn man am Ende einer Liste angelangt ist, geht man ein Feld zurück und nimmt das nächste Muster der vorigen Liste (Backtracking). Aufgrund der Konstruktion der Listen ist man sicher, daß alle Deckungsmuster auf einer Stufe kompatibel zu allen bereits verwendeten sind und keine Überzahldeckung auf Feldern mit niedrigerer Nummer entsteht.

Nun ist noch eine kleine Komplikation zu beachten. Im Verlauf der Rekursion kann es zwar sein, daß Felder, die eine Figur erfordern, besetzt werden, muß aber nicht. Um dieses sicherzustellen, wird jeweils bevor man zum nächsten Feld übergeht, eine eventuell bestehende Anforderung durch Setzen einer kompatiblen Figur aufgelöst.

Mit diesem Verfahren findet man alle Lösungen genau einmal, wenn man die gespiegelten oder gedrehten Varianten mitzählt. Die symmetrischen Versionen werden dann in einem weiteren Arbeitsgang aussortiert.

Eine kleine Optimierung besteht darin, doppelte Deckungsmuster auszusondern. Die Muster von König und Dame sind im Fall einer völlig eingeschlossenen Dame identisch, ebenso die des Läufers auf der ersten Reihen mit den Bauern. Ich verwende in diesen Fällen den König oder den Läufer. Dies wirkt sich natürlich auf die Zahl der Lösungen aus. Eine weitere Besonderheit bilden Bauern auf der letzten Reihe. Die decken keinerlei Felder und werden nur gesetzt, wenn sie zum Blocken einer fernwirkenden Figur erforderlich sind.

Im Falle von Aufgaben mit mehrfachen Deckungen kann man wie oben vorgehen und für jedes Feld die zugeordneten Deckungsmuster solange addieren, bis der gewünschte Deckungsgrad erreicht ist.

Zusätzlich werden eingangs gleich alle geeigneten Kombinationen von Mehrfachdeckungen hergestellt und bei Bedarf verwendet. Ansonsten geht man wie bei den einfachen Deckungen vor. Bei mehrfachen Deckung muß weiterhin beachtet werden, daß keine redundanten Lösungen durch Vertauschen der Muster eines Feldes entstehen.

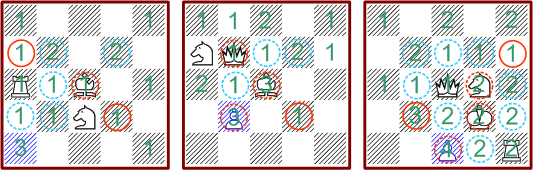Beispiele:
Die drei Muster zeigen drei- oder vierfache Mehrfachdeckungen, die sich jeweils auf das blau markierte Feld beziehen. Sie sind durch Addition von einfachen Deckungsmustern entstanden. Man beachte die gepunkteten roten Ringe, welche Figurenanforderungen bezeichnen, welche bereits innerhalb der Anordnung des Deckungsmusters aufgelöst sind.

Ich weiß nicht, ob dieses Verfahren optimal ist. Es liefert jedenfalls brauchbare und vollständige Ergebnisse und ist nicht nur für rechteckige Bretter, sondern für jede Form im Quadratgitter geeignet. Zusätzlich kann für jedes Feld ein verschiedener Deckungsgrad vorgegeben werden.

Impressum