On chessboards of various sizes we place white chess pieces, that every empty or occupied cell will be attacked exactly once. It is allowed to use any number of pieces.
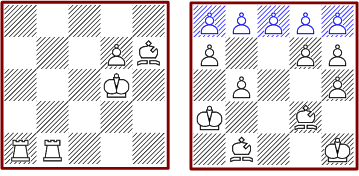
There are 27 different solutions; two of them are with four chess pieces, 6 with five, 11 with six, 4 with seven and 4 with eight pieces. The diagram shows the minimal and a maximal position:

The solution in the middle is the only one without pawns.
The 5*5 board is a little more interesting. There is a single solution with five pieces and there is none which has any symmetry and none without pawns. The total number of solutions is 16. There are 4 with six, one with seven, 7 with eight and 3 with nine pieces.
The diagram shows the minimal and a maximal solution. With the maximal configuration you can optionally place pawns on the last row, which have no impact on the attack count of any cell and therefore are ignored by the solution algorithm. It's up to you counting them or not. Here is the list of all solutions .
There is a lot more action on the 6*6 board. The minimal configuration consists of eight pieces and has three similar variants.

As already explained with the solution algorithm, pawns are not counted, if you can substitute them by bishops, otherwise there are more solutions. The solution on the left is the only one without pawns. The distribution of the solution by the number of pieces used is as follows:
| Pieces | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Solutions | 3 | 0 | 5 | 17 | 38 | 40 | 70 | 63 | 45 | 11 | 3 |
The total number is 295 with 24 symmetrical ones.
list of all solutions
The next picture shows a nice symmetrical solution with 18 pieces. Six additional and meaningless pawns can be set on the last row.

Boards with odd number of rows seem to have fewer solutions as the ones with even numbers. The 7*7 board has no solutions without pawns as well. The two minimal piece solutions are very similar:
| Pieces | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Solutions | 2 | 5 | 10 | 3 | 5 | 9 | 9 | 8 | 4 | 11 | 2 | 13 | 32 | 23 | 3 |
The total number is 139 and 8 are symmetrical.
list of all solutions
Now we have arrived at the size of the classical chessboard. Again there are no solutions without pawns. Furthermore there is none containing a queen. The two minimal configurations consist of 12 pieces.
Note that the bishops on a1 and h1 are exchangeable with pawns at the same positions. I count this as one solution only.
| Pieces | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| Solutions | 2 | 4 | 14 | 14 | 33 | 37 | 42 | 40 | 45 | 43 | 48 | 7 | 12 | 10 | 0 | 2 |
The total number is 353 and 39 of them are symmetrical.
list of all solutions
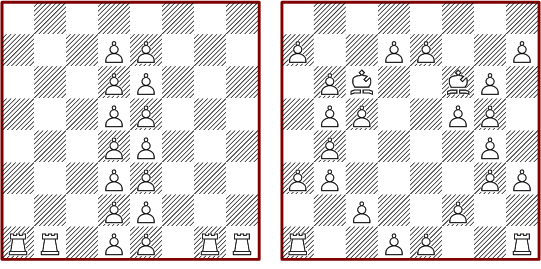
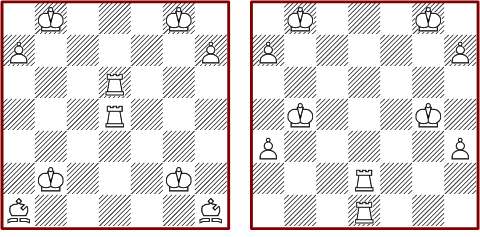
This diagram shows two selected symmetrical solutions.
This configuration consists of 19 pieces. It's the smallest I have found so far after 1200+ computing hours.

Not yet investgated.
With larger boards we leave the region where a complete computation of all solutions is possible. But there a some structures which are extensible to larger boards. The configuration with rooks and pawn in one of the above diagrams gives rise to this idea:
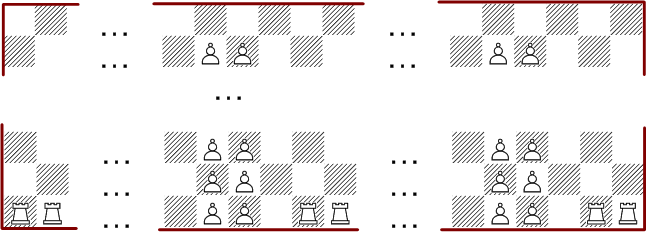
With this method we can construct a solution with single attack for all rectangular boards with 2 + n * 6 columns. Adding optional three columns at the sides you can extend the solutions to 2 + n * 3 columns, if there are enough rows.
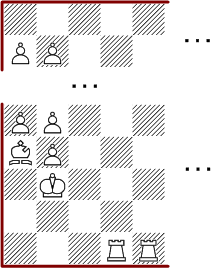
The next construction is good for all rectangles with seven columns. The middle part can repeat as often as necessary and one of the top parts completes the solution to the required number of rows. The two rows with rooks can be placed between any of the other building blocks. Another variation appears, if the top part with three rows is omitted. I try the conjecture that these solutions are minimal for every such rectangle.
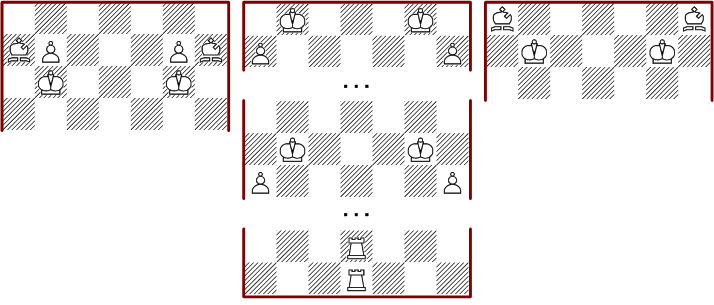
A second construction method also solves all seven-column rectangles, but uses a lot more pieces. There are some variants, if you place the rooks at the bottom or add an empty row below the kings or both. Furthermore you can place one or more of the king bishop and pawn patterns above or below the rooks in various sizes. This is similar to the three-column extension in the first construction.
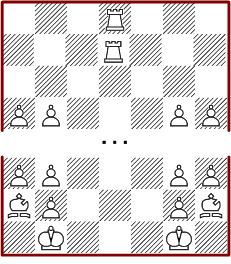
If the two rooks are placed on one row side by side, we get with a similar construction for all rectangles with eight columns. If you completely leave the rooks, rectangles with six columns are created. This works for both of the above methods, because the rooks are only loosely connected with the rest of the construction. An example is the solutions shown in the 8*8 section.
Are there more extensible solutions ?
The beginning of the series of minimal 3*n boards:
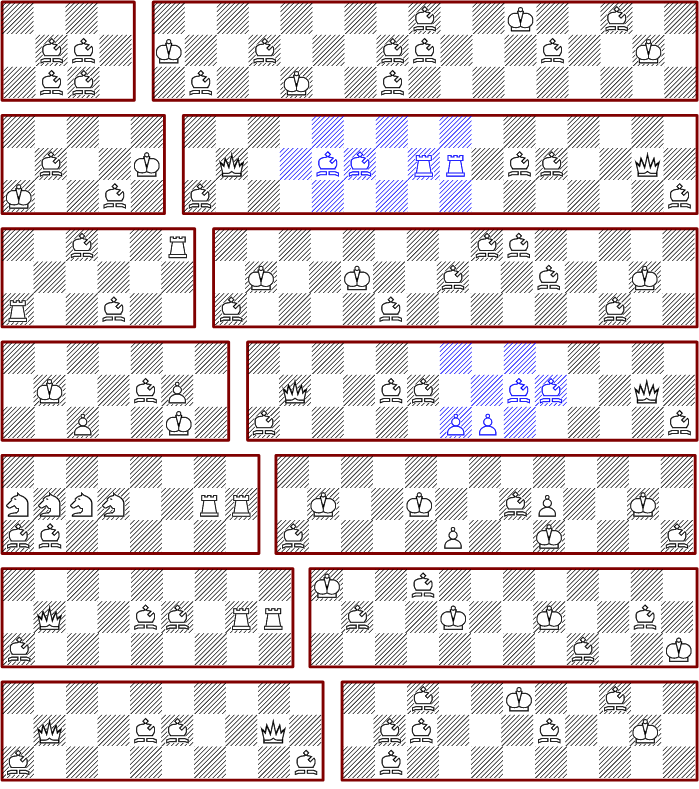
Starting from the arrangements 3*8 und 3*16 you can generate solutions for (8|9|10)+a*6 columns. The blue marked building blocks of two rooks and two bishops can occur multiple times. Because this solutions consist no pawns, they are also valid for n*3 rectangles. The configuration 3*14 shows an additional extension with two pawns and to more bishops and therefore four columns. With this generic pattern all rectangles with three rows have a solution of such type, if the number of columns is large enough. It'v very likely that these solutions are all minimal.
 All
solutions without pawns of the horizontal rectangles are of course solutions
vertical ones too. But nevertheless the problems have very different properties.
The 5*3 rectangle has a minimal solution with only three pieces, where the 3*5
rectangle needs four pieces.
All
solutions without pawns of the horizontal rectangles are of course solutions
vertical ones too. But nevertheless the problems have very different properties.
The 5*3 rectangle has a minimal solution with only three pieces, where the 3*5
rectangle needs four pieces.
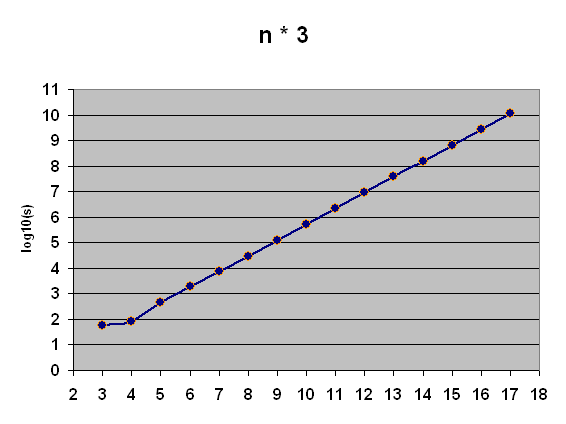
When looking at the solution numbers of the horizontal and vertical orientation, we find huge differences. Note that the solution numbers of n*3 rectangles are very near a series, where every step is four times of the previous one. The below diagram with logarithmic scale shows that this behaviour is surprisingly regular.
| Size | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ... |
| Minimal Pieces | 2 | 4/3 | 4 | 4 | 5 | 6 | 6 | 6 | 8 | 8 | 9 | 10 | 10 | |
| Solutions w/o pawns | 10 | 9 | 2 | 24 | 8 | 8 | 22 | 56 | 32 | 24 | 32 | 89 | 140 | |
| Horizontal Solutions | 34 | 19 | 18 | 74 | 108 | 77 | 139 | 746 | 1086 | 948 | 1638 | 4103 | 5728 | |
| Vertical Solutions | 34 | 81 | 440 | 1884 | 7691 | 30090 | 124902 |
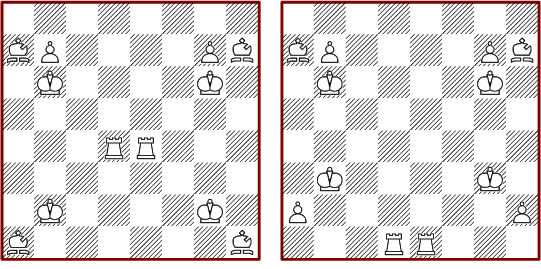
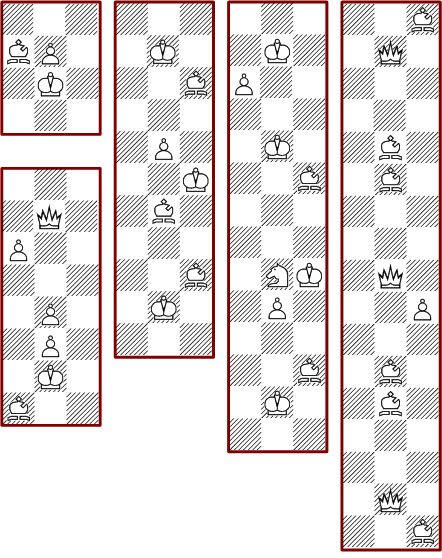
The following picture shows some minimal solutions for 4*n boards:
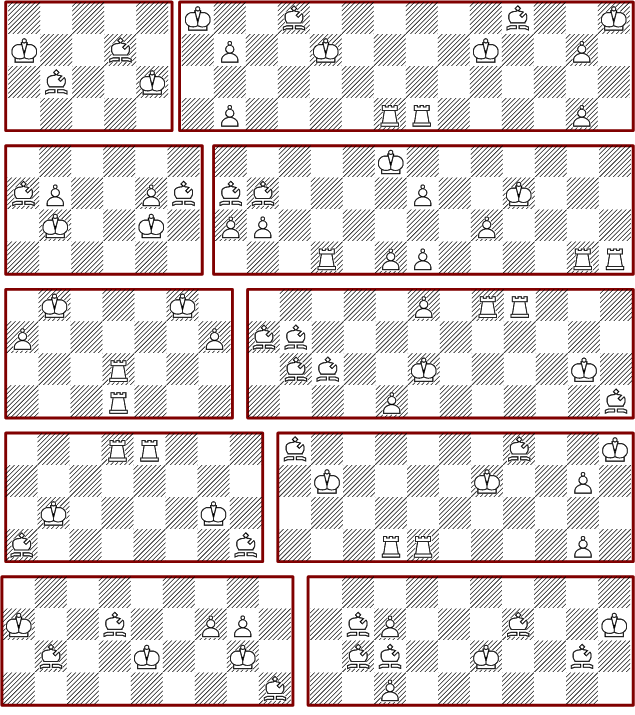
You can easily see that these solutions for n*4 boards can be extended to all larger boards with four columns.
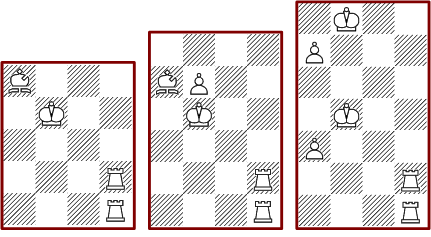
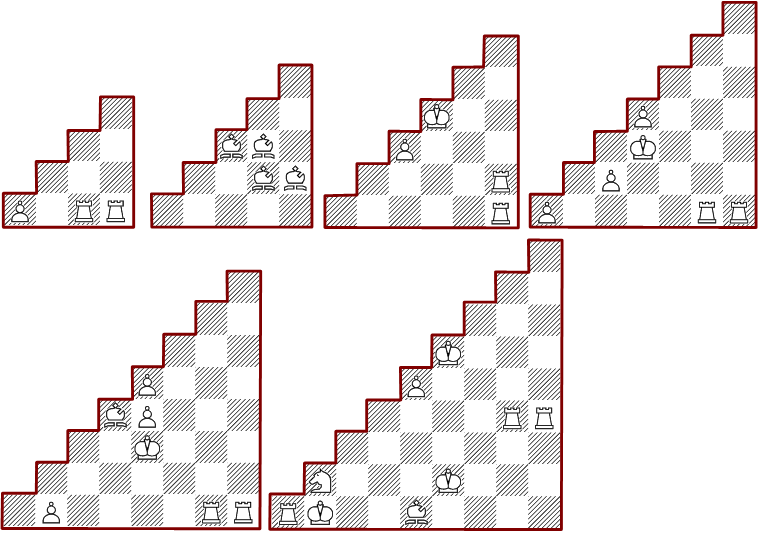
The diamond shaped form has solutions too. The minimal arrangement of the three-step form is selected from 104 solutions, the four-step form has 1334 and the five-step diamond has 49.452 different solutions.
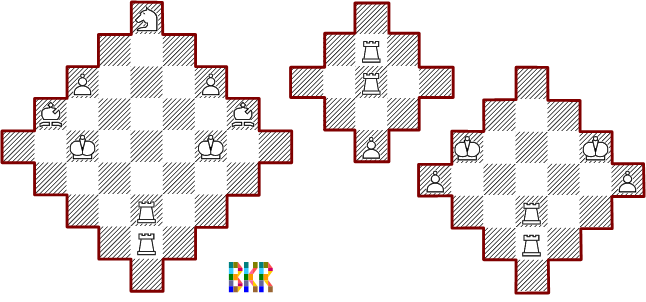
These are minimal arrangements of triangle forms: