On chessboards of various sizes we place white chess pieces, that every empty or occupied cell is attacked exactly twice. It is allowed to use any number of pieces. Compared with the single attack patterns we see various different forms and a large number of solutions.
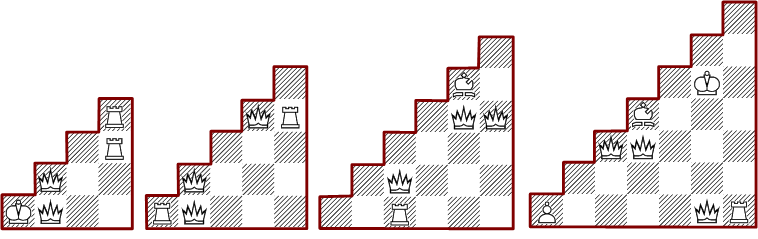
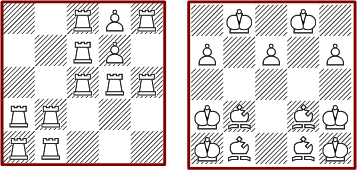
The set of 1242 different solutions contains 34 using only the main pieces. The picture below shows the four minimal solutions with six pieces and one of the maximal with 14 pieces.

There is one fully symmetric pattern and two doubly mirror symmetric.

Two remarkable solutions consist only of knights and there is a unique one with queens and pawns.
The distribution of pieces is as follows:
| Pieces | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Solutions | 4 | 9 | 59 | 147 | 324 | 336 | 264 | 85 | 14 |
The total number is 1242 with 49 symmetric solutions.
list of all solutions
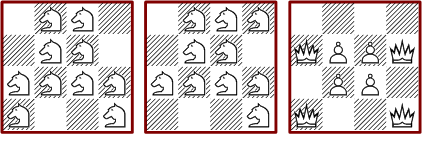
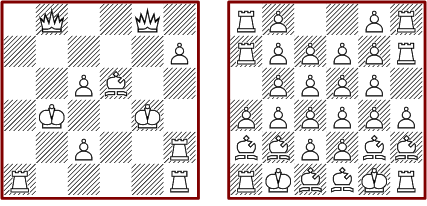
There are four minimal solutions with eight pieces. The marked rooks in the second picture have two alternative positions. The maximal pattern on the right is one of many.
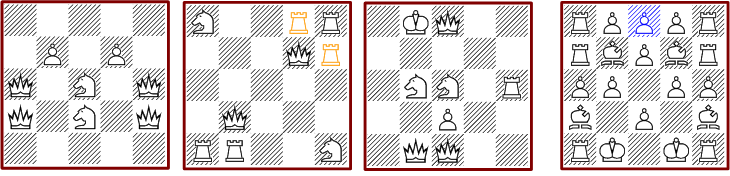
Out of the many solutions there are only ten without pawns. Only one of these has no symmetry.
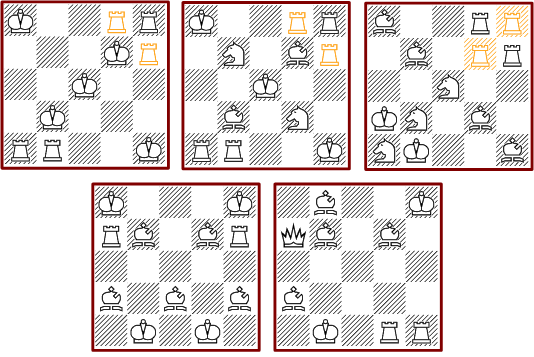
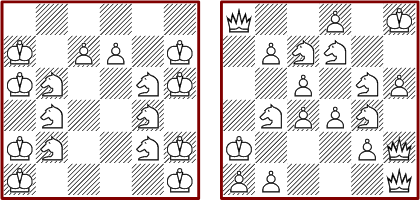
The next two diagrams show patterns that are unique with respect to the used piece types. The solution with the rooks is especially important as we will see in the section »Extensible Solutions«.
The distibution table shows that solutions with many pieces are as hard to find as the ones with few pieces.
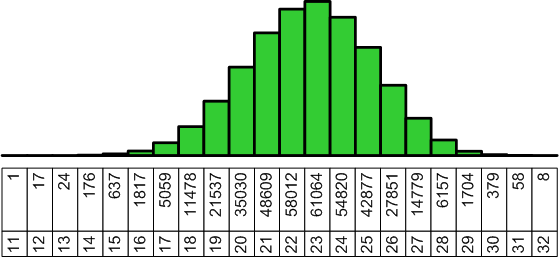
| Pieces | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Solutions | 4 | 13 | 20 | 115 | 287 | 581 | 830 | 929 | 691 | 371 | 172 | 66 | 9 |
The total number is 4088, where 263 are symmetric.
list of all solutions (0,25MB)
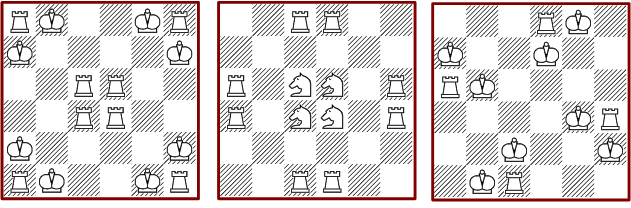
In case of double attacks the number of solutions grows extremely with the board size. Fortunately the solution set for the 6*6 is in reach of my computation capacity. The minimal pattern consists of eleven pieces and is unique! There are many maximal patterns with 32 pieces.
The number of solutions without pawns is 12, which is a surprising
small number.
There are two fully symmetric patterns and one is windmill symmetric.
Moreover there are eight mirror or rotation symmetric solutions.
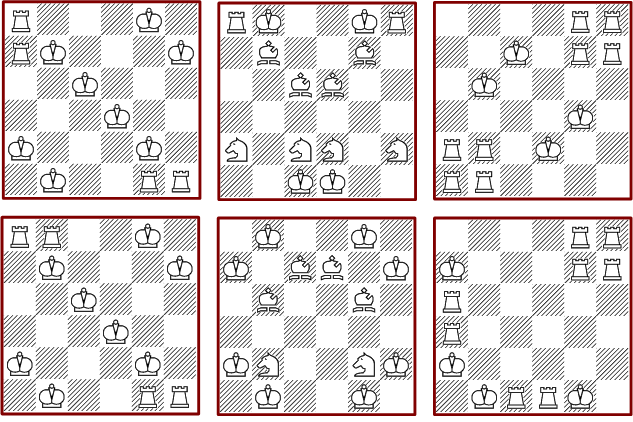
Two more solutions with rooks only are basis of extensible solutions (see further below).
The next picture shows selected solutions which are unique with respect to the used pieces.
The distribution of solutions by the number of pieces used is shown here in graphical form. You can see clearly that the distribution function is very regular. I think this points towards some general property of the problem class.

The total number of solutions is 392,091, with 658 symmetric ones.
The search tree is already very deep, so I could get only partial results.
The starting positions ![]() B3
and
B3
and ![]() C2
generate already +25.000 solutions. All of them use at least 21 pieces, which
is more than the corresponding extensible solution needs.
C2
generate already +25.000 solutions. All of them use at least 21 pieces, which
is more than the corresponding extensible solution needs.
Much more to do.
Not yet investigated.
The following extensible solutions for doubly attack patterns all stem from blocks of four rooks.
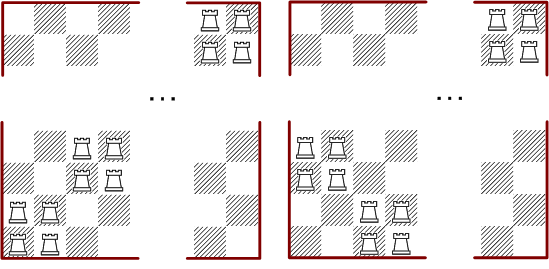
With this method we can construct double attack patterns for all quadratic boards with an even number of cells. Because the direction of the diagonal orientation of partial patterns can be mixed, we get a whole family of extensible solutions. All are based on the same
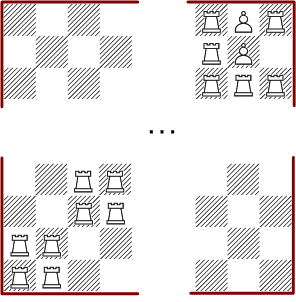
Each of the above solutions can be extended by three rows and columns as shown in the diagram. Now we have solutions for all odd quadratic boards too.
Are there more extensible solutions ?
Some of the minimal 3*n boards are also solutions of n*3 boards. Because of the pawns the boards 8*3, 9*3 and 11*3 are exceptions. The 8*3 board needs one more piece than the corresponding horizontal version.
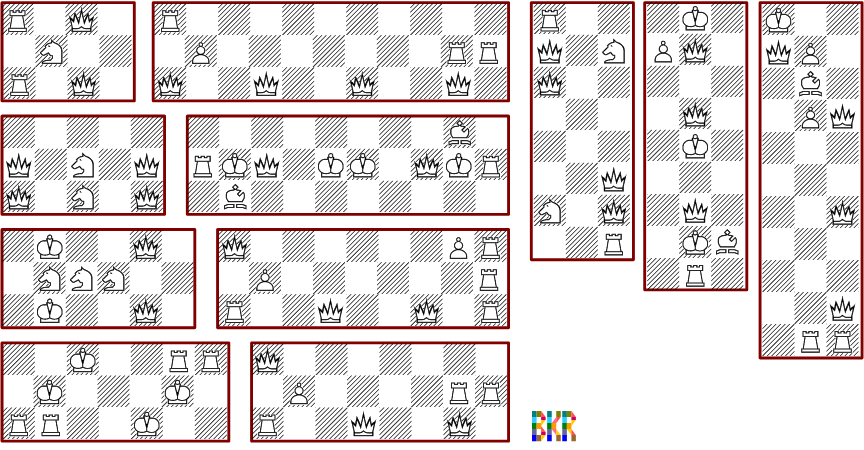
The following picture shows some minimal solutions for 4*n boards:
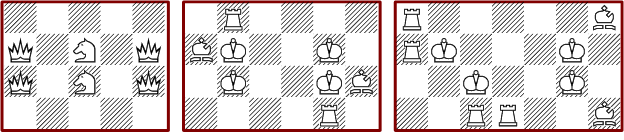
Minimal arrangements for diamond shapes:
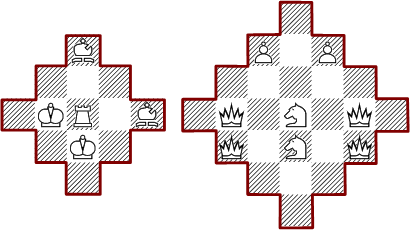
Minimal arrangements for triangle shapes: