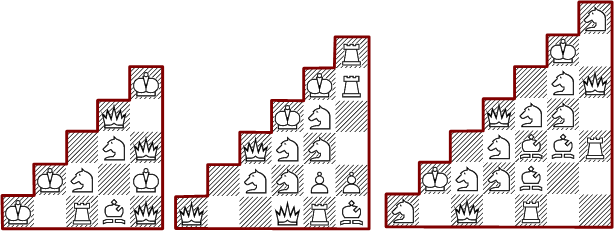
On chessboards of various sizes we place white chess pieces, that every empty or occupied cell is attacked exactly three times. It is allowed to use any number of pieces. The complexity of the triple attack problem is much larger than the double and single attack. The 6*6 board is already at the edge of my computation capacity.
The 744 different solutions of the 4*4 board contain 121 with only main pieces and 623 solutions with pawns. There is a unique minimal pattern with eight pieces.

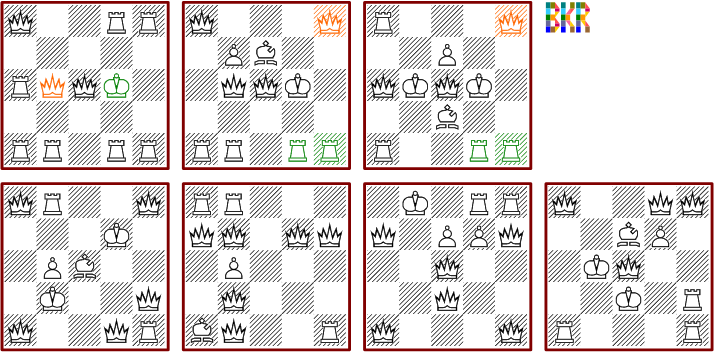
Only with the 4*4 board there are solutions with pieces placed on all cells. The following picture shows all solutions of that kind.

Distribution of piece numbers:
| Pieces | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Solutions | 1 | 6 | 25 | 84 | 177 | 204 | 164 | 65 | 18 |
Total number of solutions is 744 with 57 symmetric ones.
list of all solutions
The next diagram shows all ten minimal solutions with eleven pieces. The pieces marked coloured can be exchanged.
There are 425 solutions without pawns, that is 1.5%. The next two diagrams show patterns that are unique with respect of the used pieces.

Distribution by piece number:
| Pieces | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| Solutions | 10 | 24 | 128 | 553 | 1667 | 3282 | 5423 | 6365 | 5846 | 3823 | 1779 | 328 |
The total number of solutions is 29,228, with 30 symmetric ones.
list of all solutions (ZIP 0,3MB)
The number of solutions for triple attacks on this board is huge, so there are only partial results so far. The diagram shows a pattern with 16 pieces. This is the best minimal solution I know.

Not yet investigated.
There no known extensible solution for triple attacks.
The minimal rectangular 3*n boards, also minimal for n*3 ...
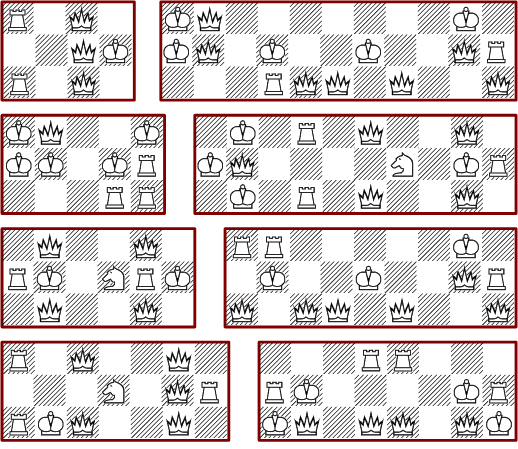
The following picture shows some minimal solutions for 4*n boards:
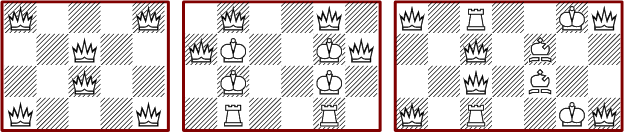
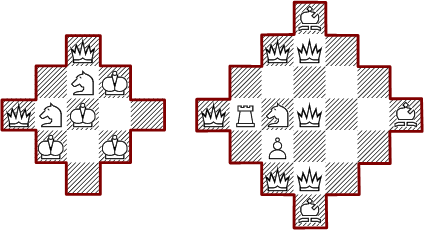
The next diamond shaped forms have 97 and 134.717 different solutions, where the shown minimal configurations are unique.
The minimal results for solutions for triangle forms are shown in next picture. Note that the four-step triangle has no solution.