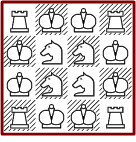
This time we place white pieces on chessboards of various sizes, that every empty or occupied cell is attacked exactly four times. It is allowed to use any number of pieces. Computations get easier compared to triple attack problems and the resulting solution numbers are small.
This is the only possible pattern with quadruple attacks on a 4*4 board. The solution is perfectly symmetric.

All eleven possible patterns of chess pieces that attack all cells four times on a 5*5 board are shown in the next picture. The minimal number of pieces is nineteen. None of the solutions contains any pawns. It's interesting that a group of five knights is part of each pattern.
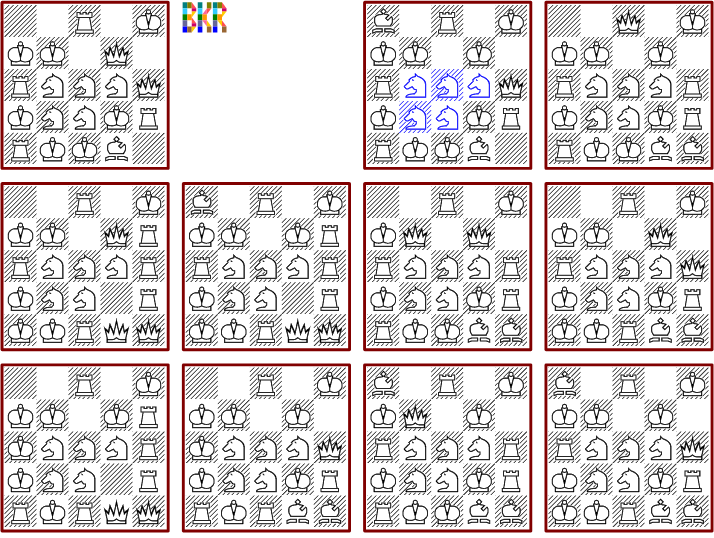
With the 6*6 board there are only eight patterns that attack every cell exactly four times. The small number is a bit surprising and is even smaller than the 5*5 board number. One of the solutions consists of 26 pieces, all others need 28 to 30 pieces. The minimal solution and three others are symmetric. Six of the patterns have a nice ring structure of knights in the centre.
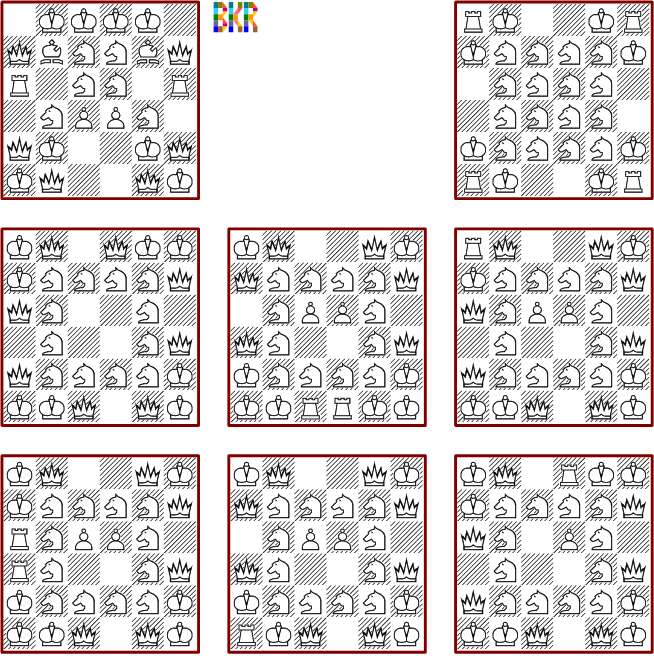
Not yet investigated.
There no known extensible solution for quadruple attacks.
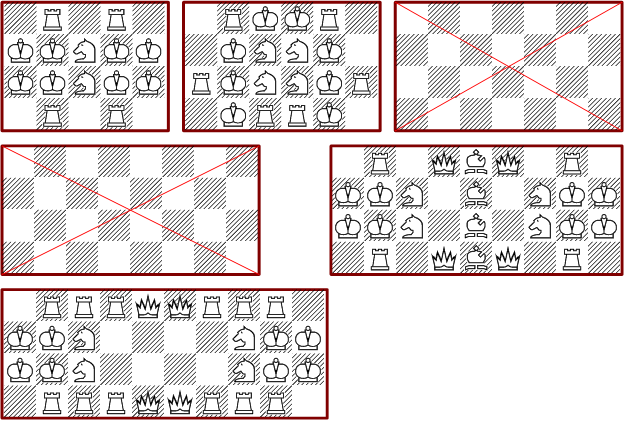
All shown minimal 3*n boards are also minimal solutions of the corresponding n*3 boards. Some of the rectangles have no solutions as has been proved by exhaustive search.
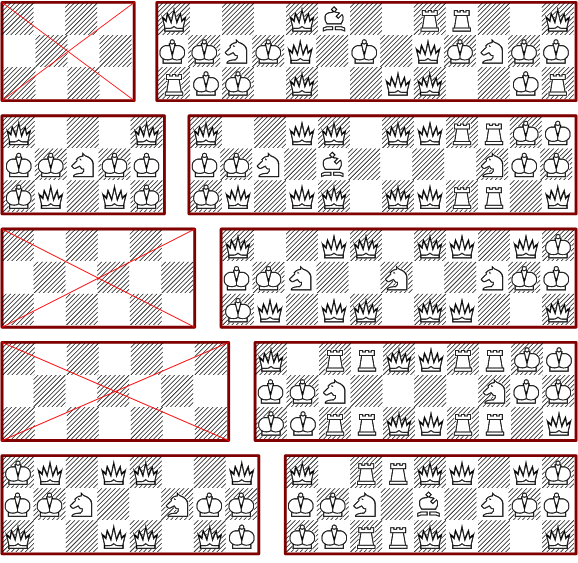
The following picture shows some minimal solutions for 4*n boards:
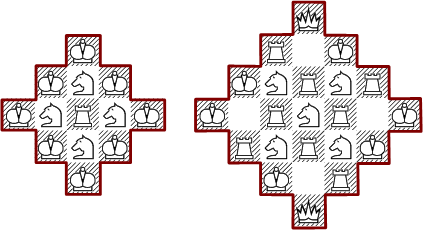
Minimal arrangements for diamond shapes:
It is impossible to attack all cells of triangle shapes four times. It's easy to see, if you try to cover the corner cells.